A máquina mais importante da sociedade moderna nunca foi construída

Outro dia, conversando com meu sobrinho, ele disse que quando ele, Alan, inventou as máquinas de Turing em 1936, Alan Turing também inventou a computação moderna.

Bom, a computação é um conceito familiar que a maioria de nós entende intuitivamente. Tome a função f(x) = x + 3. Quando x é três, f(3) = 3 + 3. Seis. Fácil, não é? Parece óbvio que esta função é computável. Mas algumas funções não são tão simples e não é tão fácil determinar se elas podem ser computadas, o que significa que elas podem nunca nos dar uma resposta final.

Em 1928, os matemáticos alemães David Hilbert e Wilhelm Ackermann propuseram uma questão chamada Entscheidungsproblem (“problema de decisão”). Com o tempo, sua pergunta levaria a uma definição formal de computabilidade, que permitiu aos matemáticos responder a uma série de novos problemas e lançou as bases para a ciência da computação teórica.

A definição veio de um estudante de pós-graduação de 23 anos chamado Alan Turing, que em 1936 escreveu um artigo seminal que não apenas formalizou o conceito de computação, mas também provou ser uma questão fundamental em matemática e criou a base intelectual para a invenção da computador eletrônico.

O grande insight de Turing foi fornecer uma resposta concreta à questão da computação na forma de uma máquina abstrata, mais tarde chamada de máquina de Turing por seu orientador de doutorado, Alonzo Church. É abstrato porque não existe (e não pode) existir fisicamente como um dispositivo tangível. Em vez disso, é um modelo conceitual de computação: se a máquina pode calcular uma função, então a função é computável.

Veja como funciona.

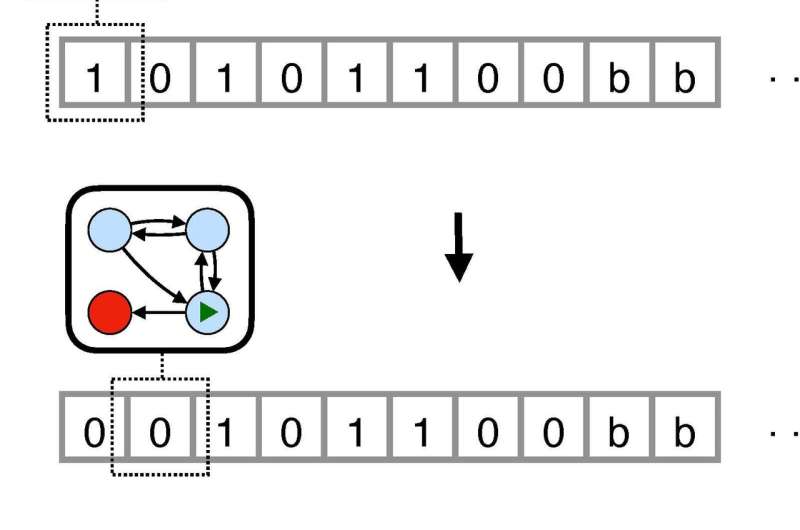
Uma máquina de Turing pode ler e alterar símbolos em uma fita infinitamente longa, conforme ditado por uma tabela de regras. A fita é composta de “células”, que podem armazenar exatamente um símbolo, e a máquina lê e reescreve o conteúdo das células com uma cabeça de fita. Cada regra na tabela determina o que a máquina deve fazer com base em seu estado atual e no símbolo que está lendo. A máquina pode entrar em um estado final (“estado de aceitação” ou “estado de rejeição”) no qual ela para, aceitando ou rejeitando a entrada. Ou cai em um loop infinito e continua lendo a fita para sempre.

A melhor maneira de entender uma máquina de Turing é considerar um exemplo simples.

Vamos imaginar um que seja projetado para nos dizer se uma determinada entrada é o número zero. Usaremos o número de entrada 0001 acompanhado de símbolos em branco (#), então “#0001#” é a parte relevante de nossa fita. A máquina começa no estado inicial, que chamaremos de q0. Ele lê a célula mais à esquerda em nossa fita e encontra um espaço em branco. As regras dizem: “Quando no estado q0, se o símbolo for #, deixe-o como está sem modificação, mova uma célula para a direita e mude o estado da máquina para q1”. Após esta etapa, a máquina está no estado q1, e seu cabeçote está lendo o segundo símbolo, 0.

Agora procuramos uma regra que se aplique a essas condições.

Encontramos uma que diz: “Permaneça no estado q1 e mova a cabeça uma célula para a direita”. Isso nos deixa na mesma posição (no estado q1, lendo “0”), então continuamos nos movendo para a direita até que a cabeça finalmente leia um número diferente, o 1. 

Quando consultamos a tabela novamente, encontramos uma nova regra: “Se encontrarmos um 1, transição para q2, que é um estado ‘rejeitado’.” A máquina para, respondendo “Não” à pergunta original, “É '0001' zero?”

Se, em vez disso, a entrada for “#0000#”, a máquina encontrará um # após todos esses zeros. Ao consultar a tabela, encontramos uma regra que diz que isso significa que a máquina entra no estado q3, um estado de “aceitar”. Agora a máquina responde “Sim” à pergunta “É '0000' zero?”

Com sua máquina abstrata, Turing estabeleceu um modelo de computação para responder ao Entscheidungsproblem, que pergunta formalmente:  Dado um conjunto de axiomas matemáticos, existe um processo mecânico – um conjunto de instruções, que hoje chamaríamos de algoritmo – que sempre pode determinar se uma determinada afirmação é verdadeira?

Digamos que queremos encontrar um algoritmo que nos diga se uma determinada posição no xadrez é possível. Aqui, os axiomas são as regras do xadrez que regem os movimentos legais. Podemos seguir uma sequência finita de procedimentos passo a passo para chegar a essa posição? Embora algumas posições possam levar mais tempo do que o nosso tempo de vida para analisar – um algoritmo pode gerar todas as posições possíveis e comparar cada uma delas com a entrada – tais algoritmos existem no jogo de xadrez. Como resultado, dizemos que o xadrez é “decidível”.

John Conway

No entanto, em 1936, Church e Turing - usando métodos diferentes - provaram independentemente que não há uma maneira geral de resolver todas as instâncias do Entscheidungsproblem. Por exemplo, alguns jogos, como o Game of Life de John Conway, são indecidíveis: nenhum algoritmo pode determinar se um determinado padrão aparecerá a partir de um padrão inicial.

Turing mostrou que uma função é computável se existe um algoritmo que pode executar a tarefa desejada. Ao mesmo tempo, ele mostrou que um algoritmo é um processo que pode ser definido por uma máquina de Turing. Portanto, uma função computável é uma função que possui uma máquina de Turing para computá-la. Isso pode parecer uma maneira tortuosa de definir computabilidade, mas é o melhor que temos. “Não é como se você tivesse a opção de defini-lo de outra maneira”, disse Michael Sipser, cientista da computação teórico do Instituto de Tecnologia de Massachusetts. “Acho que é comumente aceito que a tese de Church-Turing diz que a noção informal de algoritmo corresponde ao que qualquer modelo computacional ‘razoável’ pode fazer.” Outros matemáticos criaram diferentes modelos de computação que parecem bem diferentes na superfície, mas na verdade são equivalentes: Eles podem fazer qualquer cálculo que as máquinas de Turing podem fazer e vice-versa.

Apenas alguns anos depois de Kurt Gödel ter provado que a matemática era incompleta, Church e Turing mostraram com este trabalho que alguns problemas em matemática são indecidíveis – nenhum algoritmo, por mais sofisticado que seja, pode nos dizer se a resposta é sim ou não. Ambos foram golpes devastadores para Hilbert, que esperava que a matemática tivesse respostas organizadas e idealizadas. Mas talvez seja melhor assim: se existisse uma solução geral para o Entscheidungsproblem, isso significaria que todos os problemas matemáticos poderiam ser reduzidos a simples cálculos mecânicos.

Além de responder a essas questões fundamentais, a máquina de Turing também levou diretamente ao desenvolvimento dos computadores modernos, por meio de uma variante conhecida como máquina de Turing universal. Este é um tipo especial de máquina de Turing que pode simular qualquer outra máquina de Turing em qualquer entrada. Ele pode ler uma descrição de outras máquinas de Turing (suas regras e fitas de entrada) e simular seus comportamentos em sua própria fita de entrada, produzindo a mesma saída que a máquina simulada produziria, assim como os computadores de hoje podem ler qualquer programa e executá-lo.  Em 1945, John von Neumann propôs uma arquitetura de computador - chamada de arquitetura von Neumann - que tornou possível o conceito universal da máquina de Turing em uma máquina da vida real.

Alan Turing 

Quando Sanjeev Arora, um teórico cientista da computação da Universidade de Princeton, ensina esse conceito, ele enfatiza um quadro filosófico mais amplo. "Existem duas noções de 'universal'", disse ele. “Uma noção do universal é que ele pode operar qualquer outra máquina de Turing. Mas a outra noção maior de ‘universal’ é que ele pode executar qualquer computação que você criar no universo.” No mundo da física clássica, qualquer processo físico pode ser modelado ou simulado por meio de algoritmos, que, por sua vez, podem ser simulados por uma máquina de Turing.

Outra variante notável e cada vez mais útil é a máquina de Turing probabilística. Ao contrário de uma máquina de Turing regular – que tem uma reação bem definida para cada entrada – uma máquina de Turing probabilística pode ter múltiplas reações baseadas em probabilidades. Isso significa que pode produzir resultados diferentes para a mesma entrada em momentos diferentes. Surpreendentemente, esse tipo de estratégia probabilística pode ser mais eficiente do que uma abordagem puramente determinística para certos problemas. Idéias de máquinas de Turing probabilísticas demonstraram ser úteis na prática em áreas como criptografia, otimização e aprendizado de máquina.

Essas máquinas abstratas são talvez a melhor evidência de que fazer perguntas fundamentais pode estar entre as coisas mais úteis que um cientista pode fazer.